Implementando una regresión lineal múltiple con MATLAB

En éste post utilizaremos MATLAB para encontrar el modelo lineal que describa mejor la relación entre la cantidad de dinero invertida en diversos medios de comunicación, y la cantidad de ventas que trajo consigo.

Insumos:

1. Utilizaremos la versión de MATLAB R2016a (se puede implementar en versiones del 2016 en adelante).
2. El set de datos se llama “Advertising” ,lo puedes descargar desde Kaggle en formato csv:

Advertising Data

Download Open Datasets on 1000s of Projects + Share Projects on One Platform. Explore Popular Topics Like Government…

www.kaggle.com

Manos a la obra:

Cargaremos los datos desde el directorio donde guardamos el dataset:

>>data=readtable('C:\Users\MiguelAngel01\Documents\MATLAB\Advertising.csv');

Veamos los encabezados que conforman las columnas del dataset:

>>data(1,:)ans =Var1     TV      Radio    Newspaper    Sales
____    _____    _____    _________    _____'1'     230.1    37.8     69.2         22.1

El dataset está conformado por información de cantidades (en euros, dólares quizás, no tenemos más información sobre el tipo de moneda utilizada) invertidas en medios de comunicación como “TV”, “Radio” y “Newspaper” y las ventas que trajo consigo.

Eliminaremos la columna “Var1” puesto que contiene información que no es útil para nuestro modelo.

>> data(:,1)=[];
>> data(1,:)ans = TV      Radio    Newspaper    Sales
_____    _____    _________    _____230.1    37.8     69.2         22.1

Ahora nuestro set de datos está conformado por 200 filas y 4 columnas:

>> size(data)ans =200     4

Veamos el comportamiento de la variable de respuesta (Sales) respecto a cada una de las variables predictoras (TV, Radio y Newspaper). Para ello utilizaremos gráficos de dispersión.

Para poder graficar los datos en Matlab necesitamos cambiarlos de una tabla a una matriz.

>> data_matrix=data{:,:}

Graficando “Sales ~ TV”

>> scatter(data_matrix(:,1),data_matrix(:,4),'*')
>> title('Sales~TV')
>> xlabel('TV')
>> ylabel('Sales')

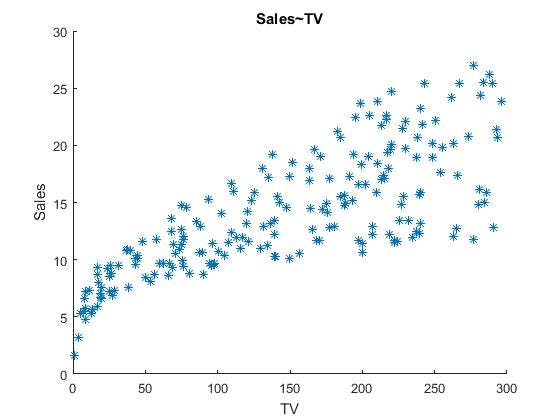
Graficando “Sales ~ Radio”

>> scatter(data_matrix(:,2),data_matrix(:,4),'*')
>> title('Sales~Radio')
>> xlabel('Radio')
>> ylabel('Sales')

Graficando “Sales ~ Newspaper”

>> scatter(data_matrix(:,3),data_matrix(:,4),'*')
>> title('Sales~Newspaper')
>> xlabel('Newspaper')
>> ylabel('Sales')

Crearemos algunos modelos con diferentes combinaciones entre las variables predictoras y la variable de respuesta.

Modelo 1: Sales ~ TV + Radio+Newspaper

>> modelspec1 = 'Sales ~ TV + Radio+Newspaper';
>> md1 = fitlm(data,modelspec1)md1 =Linear regression model:
    Sales ~ 1 + TV + Radio + NewspaperEstimated Coefficients:
                    Estimate        SE         tStat        pValue  
                   __________    _________    ________    __________   (Intercept)        2.9389      0.31191      9.4223    1.2673e-17
    TV               0.045765    0.0013949      32.809      1.51e-81
    Radio             0.18853    0.0086112      21.893    1.5053e-54
    Newspaper      -0.0010375     0.005871    -0.17671       0.85992Number of observations: 200, Error degrees of freedom: 196
Root Mean Squared Error: 1.69
R-squared: 0.897,  Adjusted R-Squared 0.896
F-statistic vs. constant model: 570, p-value = 1.58e-96

Modelo 2: Sales ~ TV + Radio

>> modelspec2 = 'Sales ~ TV + Radio';
>> md2 = fitlm(data,modelspec2)md2 =Linear regression model:
    Sales ~ 1 + TV + RadioEstimated Coefficients:
                   Estimate       SE        tStat       pValue  
                   ________    _________    ______    __________   (Intercept)      2.9211      0.29449    9.9192    4.5656e-19
    TV             0.045755    0.0013904    32.909     5.437e-82
    Radio           0.18799      0.00804    23.382     9.777e-59Number of observations: 200, Error degrees of freedom: 197
Root Mean Squared Error: 1.68
R-squared: 0.897,  Adjusted R-Squared 0.896
F-statistic vs. constant model: 860, p-value = 4.83e-98

Modelo 3: Sales ~ TV + Newspaper

>> modelspec3 = 'Sales ~ TV + Newspaper';
>> md3 = fitlm(data,modelspec3)md3 =Linear regression model:
    Sales ~ 1 + TV + NewspaperEstimated Coefficients:
                   Estimate       SE        tStat       pValue  
                   ________    _________    ______    __________   (Intercept)      5.7749      0.52534    10.993    3.1459e-22
    TV             0.046901    0.0025809    18.173    5.5076e-44
    Newspaper      0.044219     0.010174    4.3463    2.2171e-05Number of observations: 200, Error degrees of freedom: 197
Root Mean Squared Error: 3.12
R-squared: 0.646,  Adjusted R-Squared 0.642
F-statistic vs. constant model: 180, p-value = 3.95e-45

Modelo 4: Sales ~ TV

>> modelspec4 = 'Sales ~ TV';
>> md4 = fitlm(data,modelspec4)md4 =Linear regression model:
    Sales ~ 1 + TVEstimated Coefficients:
                   Estimate       SE        tStat       pValue  
                   ________    _________    ______    __________  (Intercept)      7.0326      0.45784     15.36    1.4063e-35
    TV             0.047537    0.0026906    17.668    1.4674e-42Number of observations: 200, Error degrees of freedom: 198
Root Mean Squared Error: 3.26
R-squared: 0.612,  Adjusted R-Squared 0.61
F-statistic vs. constant model: 312, p-value = 1.47e-42

Resumen de los modelos creados

Escogiendo el modelo adecuado

Tomaremos el modelo con el p-valor y el RMSE menor. Así como el valor mayor para el estadístico f, lo cual indica que las variables predictoras involucradas son las que más aportan al modelo. Por lo tanto escogeremos el modelo 2 :Sales ~ TV + Radio.

>> md2.Formulaans =Sales ~ 1 + TV + Radio

Veamos cuáles son los coeficientes que acompañan al modelo:

>> coefvals = md2.Coefficients(:,1);
>> coefvals = table2array(coefvals)coefvals =    2.9211
    0.0458
    0.1880

De manera que nuestro modelo integrado sería el siguiente:

Sales=2.9211+0.0458*TV+0.1880*Radio