Método de Newton-Raphson en Matlab
El método de Newton-Rhapson es uno de los más utilizados para dar solución a ecuaciones algebraicas y trascendentes. Clasificándose entre los métodos abiertos, es decir, aquellos que requieren uno o dos valores que no necesariamente encierren a la raíz.
Si el valor inicial para la raíz es xi, entonces se puede trazar una tangente desde el punto [xi, f(xi)] de la curva, el punto donde esta tangente cruza al eje “x” representa una aproximación mejorada de la raíz.
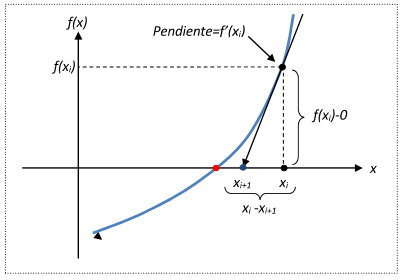
El método de Newton-Raphson se deduce a partir de esta interpretación geométrica y se tiene que la primera derivada en x es equivalente a la pendiente:
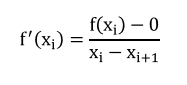
Que se arregla para obtener:
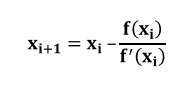
Mientras que el error aproximado porcentual lo calcularemos con la siguiente fórmula:
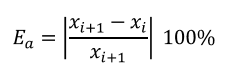
Código en Matlab
Nota: Es importante mencionar que para el siguiente código es necesario tener instalada la symbolic math toolbox, para trabajar con matemática simbólica.
Podemos crear un nuevo script en Matlab y usar el código siguiente, en cual nos permitirá ingresar la función, el punto de inicio, porcentaje de error.
El código mostrará el gráfico de la función, así como la raíz buscada.
El código mostrará el gráfico de la función, así como la raíz buscada.


Comentarios
Publicar un comentario